Príklad 1

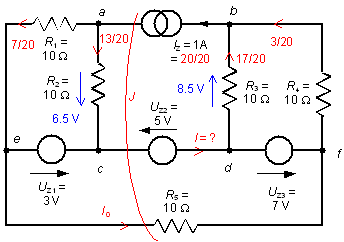
Medzi uzlami ef je napätie:

, preto

Súčet prúdov v reze J je nula:

, preto

V slučke acea: ,

preto

V slučke bfdb: ,

preto

Zo súčtu prúdov v uzloch a a b máme:

Napätia medzi uzlami potom sú:

Napätie na prúdovom zdroji:

Tento zdroj výkon dodáva.

Iný postup:

Nech uzol c je referenčný: odkiaľ priamo .

Nech uzol d je referenčný: odkiaľ priamo .

Príklad 2

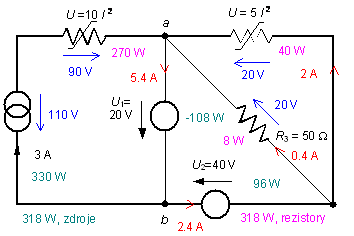
Bez riešenia sústavy rovníc. V slučke vľavo, s prúdovým zdrojom (3A) je známy prúd. Napätie na nelineárnom rezistore (90 V) sa vypočíta z jeho VA-charakteristiky. V slučke vpravo je známe napätie oboch zdrojov a preto je známe aj napätie na nelineárnom rezistore. Jeho prúd (2A) sa vypočíta z VA-charakteristiky. Ostatné – priamo z Kirchoffových zákonov a Ohmovho zákona.

Príklad 3

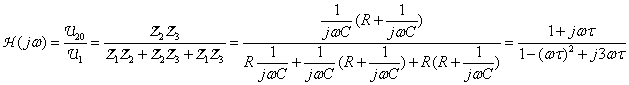keď .

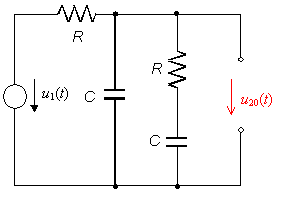
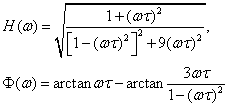
Ak bude: , ,

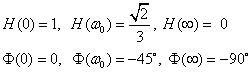
Príklad 4

Napätie nezávisí od impedancií zapojených do trojuholníka 3´3Z, je dané len výrazom v ktorom vystupujú impedancie záťaže zapojenej do hviezdy 3´Z

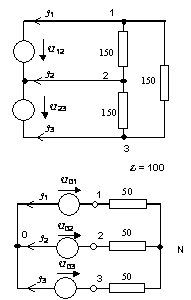
posledné platí vďaka tomu, že záťaž je súmerná.

Je teda

Výpočet napätí na impedanciách zapojených do Y

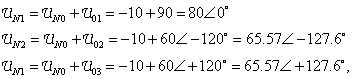
Fázory prúdov sú v záťaži Y:

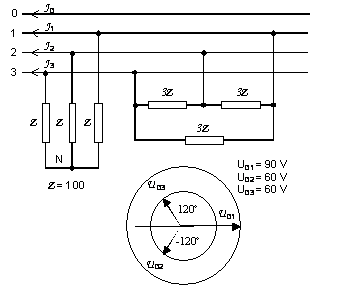
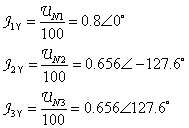
Prvá možnosť - použijeme transfiguráciu D ® Y

budeme mať namiesto trojuholníka 3´3Z, hviezdu 3´Z:

a celkovú záťaž: dve Y každú s impeadnciami 3´Z, t.j. 3´100 W

si môžeme predstaviť ako jednu Y/ s impedanciami 3´Z/2, t.j. 3´50 W

Prvá možnosť - použijeme transfiguráciu Y ® D namiesto hviezdy 3´Z

dostaneme trojuholník 3´3Z

.

Výsledná záťaž je potom akoby tvorená dvomi paralelnými D - každý z nich 3´3Z , t.j. 3´300 - čo predstavuje jeden trojuholník 3´3Z/2, t.j. 3´150.

Tento sa opäť dá transformovať na hviezdu (3´50 W).

Podľa uvedeného, obe záťaže aj Y aj D odoberajú rovnaké fázové prúdy Výsledné prúdy fáz sú teda dvojnásobné ako je uvedene vyššie.