naspäť na hlavnú stránku

Skúška z predmetu: ELEKTROTECHNIKA 1

Príklady - 50 bodov

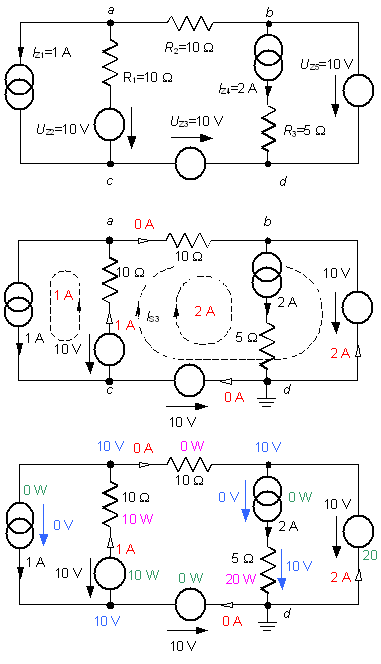Príklad 1 - (15 bodov)

Ľubovolnou metódou zostavte minimálny počet rovníc potrebných na výpočet neznámych prúdov v obvode podľa obrázku (3 body). Rovnice vyriešte (2 body). Vypočítajte a bilancujte výkon (dodaný alebo spotrebovaný) jednotlivými zdrojmi a rezistormi (8 bodov). Aj keď zvolíte slučky, alebo referenčný uzol, inak ako je doporučené na dolnom obrázku - uveďťe aj hodnoty tam vyznačených sľučkových prúdov i_s1, i_s2, i_s3, aj hodnoty tam vyznačených uzlových napätí u_ad, u_bd, u_cd (vzhľadom na vzťažný uzol "d"), bez ohľadu na to akú metódu ste pri riešení použili (2 body).

1. riešenie

v obvode sú dva prúdové zdroje (I_s1=1, I_s2=2) preto stačí jediná rovnica pre slučkový prúd I_s3 (namiesto prekreslenia obvodu môžeme zvoliť slučky podľa obrázku v strede):

I_s3(10+10)+I_s110+I_s2(10+10)+10 -10 -10 = 0

teda

20I_s3+1.10+2.(20) -10 = 0

20I_s3 = -40 s riešením: I_s3 = - 2

2.riešenie

v obvode sú známe napätia dvoch uzlov (U_cd =10, U_bd =10) preto stačí jediná rovnica pre napätie U_ad:

U_ad(1/10+1/10) -U_bd/10-U_cd/10 –1+10/10= 0

teda

U_ad2/10 -10/10 -10/10 = 0

U_ad/5 = 2 s riešením: U_ad = 10

Pri výpočte výkonov (P = UI) treba pri zdrojoch znamienkom rozlišiť či sú prúd a napätie orientované súhlasne (zdrojom spotrebovaný výkon: P<0) alebo proti sebe (zdrojom dodaný výkon: P>0). Na rezistoroch je orientácia vždy súhlasná (rezistorom spotrebovaný výkon: P >0). zhodou okolností sú v danej úlohe výkony prúdových zdrojov nulové a žiadný z výkonov napäťového zdroja nie je záporný (nemusi to vždy byť tak !).

Is1 = 1	Is2 = 2	Is3 = -2
Ucd = 10	Ubd =10	Uad = 10

PR1 = 10	PZ1 = 0	PZ4 = 0
PR2 = 0	PZ2 = 10	PZ5 = 20
PR3 = 20	PZ3 = 0	SPZ = 30
SPR = 30	Vždy platí: SPR = SPZ

Príklad 2 - (7 bodov)

Na základe merania poznáte výstupný výkon P₄ = 2 W (na rezistore 2W), poznáte v obrázku vyznačený prúd I₀ = 5 A, napätie U₃ = 9 V, a VA-charakteristiku symetrického nelineárneho prvku I/I₀ = (U/U₀)³, precházdajúcu bodom I₀ = 5 A, U₀ = 6 V. Vypočítajte pomer I₄ / I₃ (tzv. prúdový prenos) a pomer U₂ / U₁ (tzv. napäťový prenos) trojpólov T2 a T1 v zapojení podľa obrázku.

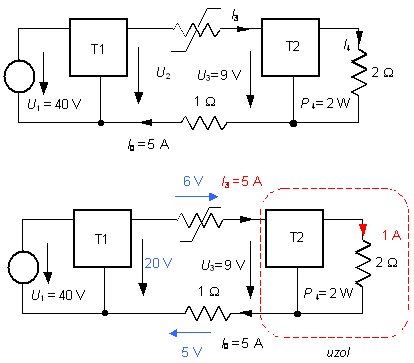
riešenie

Ak je na výstupe výkon P = RI² =2W,

pričom R = 2 W, musí byť : I₄ = 1 A.

Vzhľadom na vyznačený (zovše-obecnený) uzol platí: I₃ = I₀, teda aj I₃ = 5 A. Podiel prudov: I₄/I₃ = 1/5.

Po dosadeni (!) prúdu I₃ = 5 A do rovnice charakteristiky I/5 = (U/6)³

dostaneme priamo napätie na nelineárnom prvku U = 6 V. Zo súčtu napätí v slučke medzi T1 a T2 (6+9+5) vychádza U₂= 20 V. Preto je podiel U₂/U₁ = 20/40. A to je naozaj všetko J .

I4/I3 = 0.2

U2/U1 = 0.5

Príklad 3 - (12 bodov)

Určte časový priebeh napätia u₂(t) ak U_1max= 400 V, w =100 s^-1 a L = 2 H. Koeficient induktívnej väzby prvého páru cievok je c₁= 0.5, druhého páru cievok je c₂= 7/8. Pri riešení použite náhradu induktívne viazaných cievok dvojpólmi s nezávislými pasívnymi prvkami Z₁ ... Z₄ , a napäťovými zdrojmi U₁₂, U₂₁, U₃₄, U₄₃, riadenými prúdom (podľa obrázku dole)!

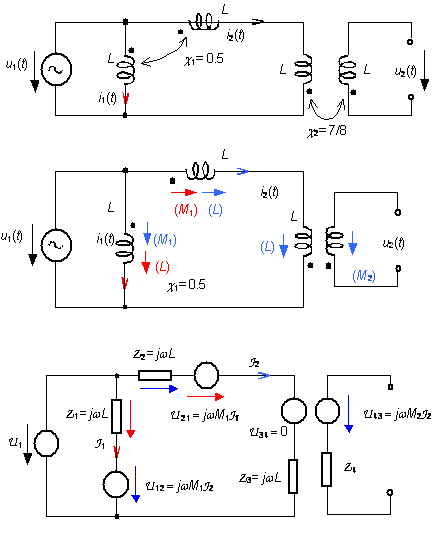
riešenie

Pretože výstup je naprázdno, napätie bude určené prúdom J₂ a vzájomnou indukčnosťou M₂ a frekvenciou w, teda: U₂ =U₄₃ (J₂) = jwM₂J₂. Druhý pár cievok sa navzájom neovplyvňuje lebo prúd tečie len jednou z nich ! (preto je U₃₄= 0). V prípade prvého páru cievok je vzájomne ovplyvňovanie započítane v oboch zdrojoch napätia riadených prúdom: U₁₂(J₂) = jwM₁J₂ a U₂₁(J₁) = jwM₁J₁. Keďže ideálny zdroj napätia U₁ je pripojený na paralelné úseky, pišeme priamo:

čo po dosadeni dáva:

a po úprave máme dve rovnice o dvoch neznámych:

s riešením:

preto U₂ = U₄₃ (J₂) = jwM₂J₂ = j175´4/(j7) = 100 V, 

časová závislosť je: u₂(t)= 100cos(100t)

Z1 = 200j	Z3 = 200j
Z2 = 200j	Z4 = 200j
U12(J2) = j100 J2	U34 (J4) = 0
U21(J1) = j100 J1	U43 (J2) = j175 J2

Príklad 4 - (16 bodov)

Udajte fázory fázových a združených napätí nesúmerného trojfázového zdroja podľa obrázku. V trojfázovej záťaži „A“ vypočítajte napätie U_OC. Stanovte komplexný výkon odoberaný zo siete dvojnásobnou (súmernou) záťažou (A+B). Pokračujte podľa návodu (postupne vypĺňajte priloženú tabulku). P₁, P₂, P₃ resp. P₁₂, P₁₃, P₂₃ - sú výkony na jednotlivých impedanciách P_A resp. P_B výkony v záťaži A resp. B a P – je komplexný výkon odoberaný zo siete. Ak poznáte menej pracné riešenie na stanovenie komplexného výkonu P, uveďte (slovne) alternatívny postup!

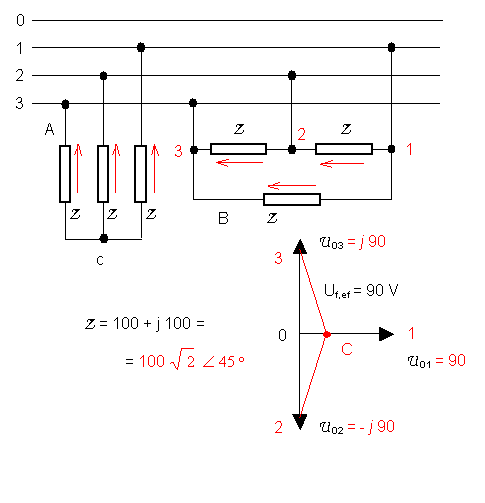
riešenie

Sústava „a“

Zdroj je nesúmerný, preto ani pri súmernej záťaži (3 x Z) nebude v sústave „A“ nulové U_0C a na impedanciách nebudú rovnaké fázory napätia ani prúdu. Pretože všetky Z  sú rovnaké a U₀₂ +U₀₃ = 0 (pozri na obrázok s fázormi napätí zdroja), je:

počítajme s efektívnymi hodnotami napätia na impedanciách,

Sústava „b“

tu sú Na impedanciách združené napätia:

Ďalej budeme s výhodou počítať podľa vzorca:

do ktorého za U_ef dosadíme abslutné hodnoty fázorov napätia na jednotlivých IMPEDANCIÁCH,

v tomto prípade:

Sústava „a“

_,

Sústava „B“

_,

UOC = 30
U01 = 90		U12 = – 90 – j 90
U02 = – j 90		U13 = – 90 + j 90
U03 = + j 90		U23 = + j 180
A B
P1 = 18 + j18	P12 = 81 + j81
P2 = 45 + j45	P13 = 81 + j81
P 3 = 45 + j45	P23 = 162 + j162
PA = 108 + j108	PB = 324 + j324
P = 432 + j432

Mimochodom, po transformácii hviezdy „A“ na trojuholník by boli všetky impedancie 3z preto je výkon v sústave „B“ 3 krát väčší ako v sústave „A“ a teda P = 4P_A.

naspäť na hlavnú stránku